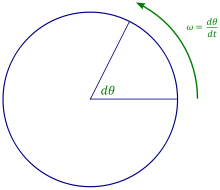
 角速度是用來描述轉動的速度以及該轉動發生當時的轉動軸方向。角速度向量的方向會在轉動軸方向上,在本例中(逆時針轉動)轉動向量是指向讀者的。
角速度是用來描述轉動的速度以及該轉動發生當時的轉動軸方向。角速度向量的方向會在轉動軸方向上,在本例中(逆時針轉動)轉動向量是指向讀者的。
角速度(Angular velocity)是在物理學中定義為角位移的變化率,描述物體轉動時,在單位時間內轉過多少角度以及轉動方向的向量,(更準確地說,是贗向量),通常用希臘字母 或
或 來表示。
來表示。
在國際單位制中,單位是弧度每秒(rad/s)。在日常生活,通常量度單位時間內的轉動週數,即是每分鐘轉速(rpm),電腦機械硬碟和汽車引擎轉數就是以rpm來量度,物理學則以rev/min表示每分鐘轉動週數。
角速度的方向垂直於轉動平面,可通過右手定則來確定,物體以逆時針方向轉動其角速度為正值,物體以順時針方向轉動其角速度為負值。
角速度量值的大小稱作角速率,通常也是用ω來表示。[1]
 位於
位於 點的質點相對於
點的質點相對於 點的角速度是由其速度向量"
點的角速度是由其速度向量" " 垂直於
" 垂直於 連線的分量來決定 。
連線的分量來決定 。
一個質點在二維平面上的角速度是最基本的。如右圖所示,假使從 點向(
點向( )質點畫一條直線,則該粒子的速度向量(
)質點畫一條直線,則該粒子的速度向量( )可分成在沿著徑向上分量(
)可分成在沿著徑向上分量( , - 徑向分量)以及垂直於徑向的分量(
, - 徑向分量)以及垂直於徑向的分量( - 切線方向分量)。
- 切線方向分量)。
由於粒子在徑向上的運動並不會造成相對於原點( )的轉動,在求取該粒子的角速度時,可以忽略水平(徑向)分量。因此,轉動完全是由切線方向的運動所造成的(如同質點在繞著等速率圓周運動),即角速度是完全由垂直(切線方向)的分量所決定的。
質點角度位置的改變率與其切線方向速度的關係式如下:
)的轉動,在求取該粒子的角速度時,可以忽略水平(徑向)分量。因此,轉動完全是由切線方向的運動所造成的(如同質點在繞著等速率圓周運動),即角速度是完全由垂直(切線方向)的分量所決定的。
質點角度位置的改變率與其切線方向速度的關係式如下:

定義角速度為 (其中
(其中 是弧度,即弧長除以半徑),而速度的垂直分量
是弧度,即弧長除以半徑),而速度的垂直分量 等於
等於 ;其中θ是向量
;其中θ是向量 與
與 的夾角,則導出:
的夾角,則導出:

在二維坐標系中,角速度是一個只有大小沒有方向的贗純量,而非純量。純量與贗純量不同的地方在於,當x 軸與y 軸對調時,純量不會因此而改變正負符號,然而贗純量卻會因此而改變。角度及角速度則是贗純量。以一般的定義,從x 軸轉向y 軸的方向為轉動的正方向。倘若座標軸對調,而物體轉動不變,則角度的正負符號將會改變,因此角速度的正負號也跟著改變。
注意:角速度的正負號及數值量取決於原點位置及座標軸方向的選定。
在三維坐標系中,角速度變得比較複雜。在此狀況下,角速度通常被當作向量來看待;甚至更精確一點要當作偽向量。它不只具有數值,而且同時具有方向的特性。數值指的是單位時間內的角度變化率,而方向則是用來描述轉動軸的。概念上,可以利用右手定則來標示角速度偽向量的正方向。原則如下:
- 假設將右手(除了大拇指以外)的手指順著轉動的方向朝內彎曲,則大拇指所指的方向即是角速度向量的方向。
正如同在二維座標系的例子中,一個質點的移動速度相對於原點可以分成一個沿著徑向以及另一個垂直徑向的分量。舉例而言,原點與質點的速度垂直分量的組合可以定義一個轉動平面,質點在此平面上的行為就如同在二維坐標系中的狀況下,其轉動軸則是一條通過原點且垂直此平面的線,這個軸訂定了角速度偽向量的方向,而角速度的數值則是如同在二維座標系狀況下求得的偽純量的值。當定義一個指向角速度偽向量方向單位向量 時,可以用類似二維坐標系的方式來表示角速度:
時,可以用類似二維坐標系的方式來表示角速度:

再加上外積的定義,則可以寫成:

一般而言,在高維空間的角速度是一個二階斜對稱的角位移張量對時間的微分。此張量具有 個獨立分量,其中"
個獨立分量,其中" "這個數字指的是在n-維內積空間中轉動李群之李代數的維度。[2]
"這個數字指的是在n-維內積空間中轉動李群之李代數的維度。[2]
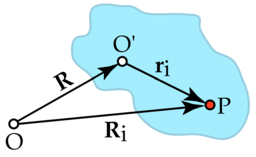
 點在剛體(以藍色表示)上的位置,
點在剛體(以藍色表示)上的位置, 是以
是以 為中心在實驗室座標系上的位置;而
為中心在實驗室座標系上的位置;而 是以
是以 為中心在剛體座標系上的位置。此剛體座標系的原點則是在實驗室座標系中的向量位置
為中心在剛體座標系上的位置。此剛體座標系的原點則是在實驗室座標系中的向量位置 上。
上。
為了處理剛體運動的問題,最好採用固定在剛體上的座標系統,然後再學習此座標系統與實驗室座標系統之間的座標轉換。如右圖所示, 為實驗室座標系統的原點,而
為實驗室座標系統的原點,而 是剛體座標系統的原點,
是剛體座標系統的原點, 與
與 之間的向量
之間的向量 。質點(
。質點( )在剛體上
)在剛體上 點的位置上,此質點在實驗室座標中的向量位置是
點的位置上,此質點在實驗室座標中的向量位置是 ,而在剛體座標中的向量位置為
,而在剛體座標中的向量位置為 。我們可以看到此質點的位置可以寫成:
。我們可以看到此質點的位置可以寫成:

剛體最重要的特徵為任意兩點之間距離不隨時間變化。這意味着矢量 的長度是不變的。根據歐拉剛體的有限旋轉定理,我們可以用
的長度是不變的。根據歐拉剛體的有限旋轉定理,我們可以用 來代替
來代替 ,其中
,其中 代表旋轉矩陣,而
代表旋轉矩陣,而 是初始時刻的質點的位置。這個替代顯得非常有意義,隨時間變化的只有
是初始時刻的質點的位置。這個替代顯得非常有意義,隨時間變化的只有 ,而不是相對矢量
,而不是相對矢量 。對於剛體就
。對於剛體就 旋轉,質點的位置可以寫為:
旋轉,質點的位置可以寫為:

就質點的速度對時間微分,可以得到質點的速度:

其中 是質點在實驗室座標中的速度,而
是質點在實驗室座標中的速度,而 是
是 點(剛體座標的原點)的在實驗室座標中的速度,故質點的速度可以寫成:
點(剛體座標的原點)的在實驗室座標中的速度,故質點的速度可以寫成:

 是角速度張量,如果我們取角速度張量的對偶,我們即可得到角速度的偽矢量。
是角速度張量,如果我們取角速度張量的對偶,我們即可得到角速度的偽矢量。
![{\displaystyle {\boldsymbol {\omega }}=[\omega _{x},\omega _{y},\omega _{z}]}](https://backend.710302.xyz/https/wikimedia.org/api/rest_v1/media/math/render/svg/c8f418d52c41570663e22f7b19a8d3a427b69cab)
而矩陣的乘法可以用外積來取代,導出:

由此可見,剛體中質點的速度可分解成兩項—剛體中某固定參考點的速度再加上一項包含該質點相對於此參考點的角速度的外積。相較於 點對於
點對於 點的角速度,這個角速度是「自旋」角速度。
點的角速度,這個角速度是「自旋」角速度。
很重要的是,每個在剛體中的質點具有相同的自轉角速度,此自轉角速度與剛體上或是實驗室座標系統的原點的選擇無關。換句話說,這是一個剛體特質所具有的真實物理量,與座標系統的選擇無關。然而剛體上的參考點相對於實驗室座標原點的角速度則和座標系統的選擇有關,為了方便起見,通常選擇該剛體的質心當作剛體座標系統的原點,這將大大地簡化以數學形式在剛體角動量上的表達。
|
|---|
| 線性(平動)的量 |
|
角度(轉動)的量 |
| 量綱 |
— |
L |
L2 |
量綱 |
— |
— |
— |
| T |
時間: t
s |
位移積分: A
m s |
|
T |
時間: t
s |
|
|
| — |
|
距離: d, 位矢: r, s, x, 位移
m |
面積: A
m2 |
— |
|
角度: θ, 角移: θ
rad |
立體角: Ω
rad2, sr |
| T−1 |
頻率: f
s−1, Hz |
速率: v, 速度: v
m s−1 |
面積速率: ν
m2 s−1 |
T−1 |
頻率: f
s−1, Hz |
角速率: ω, 角速度: ω
rad s−1 |
|
| T−2 |
|
加速度: a
m s−2 |
|
T−2 |
|
角加速度: α
rad s−2 |
|
| T−3 |
|
加加速度: j
m s−3 |
|
T−3 |
|
角加加速度: ζ
rad s−3 |
|
|
|
| M |
質量: m
kg |
|
|
ML2 |
轉動慣量: I
kg m2 |
|
|
|---|
| MT−1 |
|
動量: p, 衝量: J
kg m s−1, N s |
作用量: 𝒮, actergy: ℵ
kg m2 s−1, J s |
ML2T−1 |
|
角動量: L, 角衝量: ι
kg m2 s−1 |
作用量: 𝒮, actergy: ℵ
kg m2 s−1, J s |
| MT−2 |
|
力: F, 重量: Fg
kg m s−2, N |
能量: E, 功: W
kg m2 s−2, J |
ML2T−2 |
|
力矩: τ, moment: M
kg m2 s−2, N m |
能量: E, 功: W
kg m2 s−2, J |
| MT−3 |
|
加力: Y
kg m s−3, N s−1 |
功率: P
kg m2 s−3, W |
ML2T−3 |
|
rotatum: P
kg m2 s−3, N m s−1 |
功率: P
kg m2 s−3, W |
|




































![{\displaystyle {\boldsymbol {\omega }}=[\omega _{x},\omega _{y},\omega _{z}]}](https://backend.710302.xyz/https/wikimedia.org/api/rest_v1/media/math/render/svg/c8f418d52c41570663e22f7b19a8d3a427b69cab)
